on
Conic Sections #2
Ellipse
본 포스트에는 수식이 포함되어 있습니다. 분수 등의 수식이 정상적으로 보이지 않는 경우에는 수식을 마우스 오른쪽 버튼으로 클릭한 후 “Math Renderer”를 SVG로 바꿔주세요. (➔How-To)
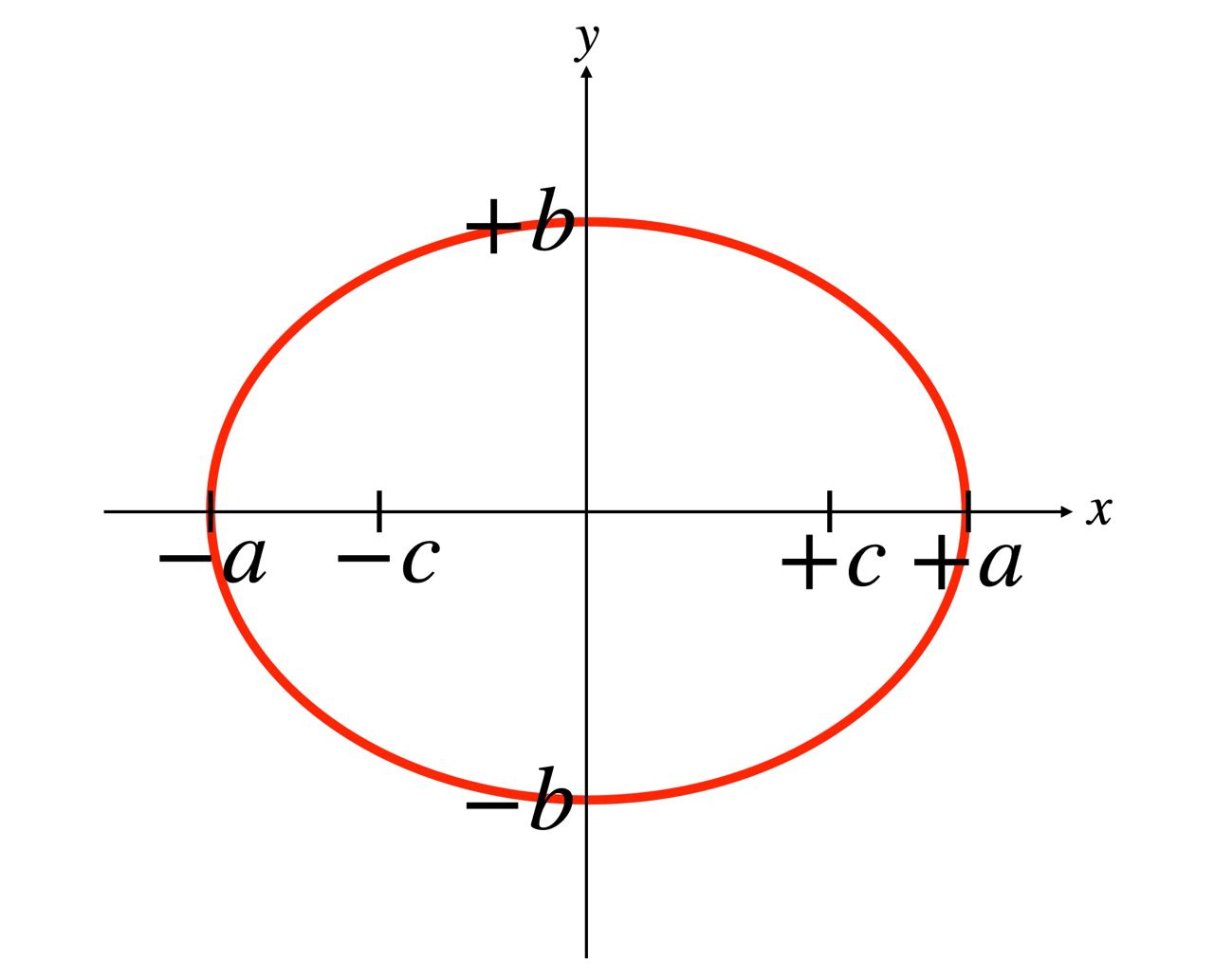
타원의 정의: 두 초점 $\mathbf{F}^{\prime}(-c,0)$, $\mathbf{F}(c,0)$로부터의 거리의 합이 일정한 점들의 집합
일정한 거리의 합을 $2a$, 타원 위의 임의의 점을 $\mathbf{P}(x,y)$라 하자.
그러면 타원의 정의에 의해 다음과 같은 등식이 성립한다.
$\overline{\mathbf{F}^{\prime}\mathbf{P}} + \overline{\mathbf{FP}} = 2a$
이 등식을 정리하면 하면 다음과 같은 타원의 방정식을 얻을 수 있다.
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
proof
$\sqrt{(x+c)^2+y^2} + \sqrt{(x-c)^2+y^2} = 2a$
$\sqrt{x^2+2cx+c^2+y^2} + \sqrt{x^2-2cx+c^2+y^2} = 2a$
$\sqrt{x^2+2cx+c^2+y^2} = 2a - \sqrt{x^2-2cx+c^2+y^2}$
$x^2+2cx+c^2+y^2 = 4a^2 - 4a \sqrt{x^2-2cx+c^2+y^2} + (x^2-2cx+c^2+y^2)$
$2cx = 4a^2 - 4a \sqrt{x^2-2cx+c^2+y^2} - 2cx$
$4a \sqrt{x^2-2cx+c^2+y^2} = 4a^2 - 4cx$
$a \sqrt{x^2-2cx+c^2+y^2} = a^2 - cx$
$a^2 (x^2-2cx+c^2+y^2) = a^4 - 2ca^2x + c^2x^2$
$a^2x^2 - 2ca^2x + a^2c^2 + a^2y^2 = a^4 - 2ca^2x + c^2x^2$
$a^2x^2 + a^2c^2 + a^2y^2 = a^4 + c^2x^2$
$(a^2-c^2)x^2 + a^2y^2 = a^4 - a^2c^2$
$(a^2-c^2)x^2 + a^2y^2 = a^2 (a^2 - c^2)$
$b^2x^2 + a^2y^2 = a^2 b^2$
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
한편 중심이 원점에 있고 반지름인 1인 단위원을 $x$축으로 $a$ 만큼, $y$축으로 $b$ 만큼 확대(또는 축소)한 도형을 생각해보자.
우선 $x$축에 대한 확대(또는 축소)를 생각해보자.
단위원 위의 임의의 점의 첫 번째 좌표값인 $x$를 수평축 방향으로 $a$배 확대한 새로운 값 $x\prime{}$은 $x$와 다음과 같은 관계를 가진다.
$x = \frac{x\prime{}}{a}$
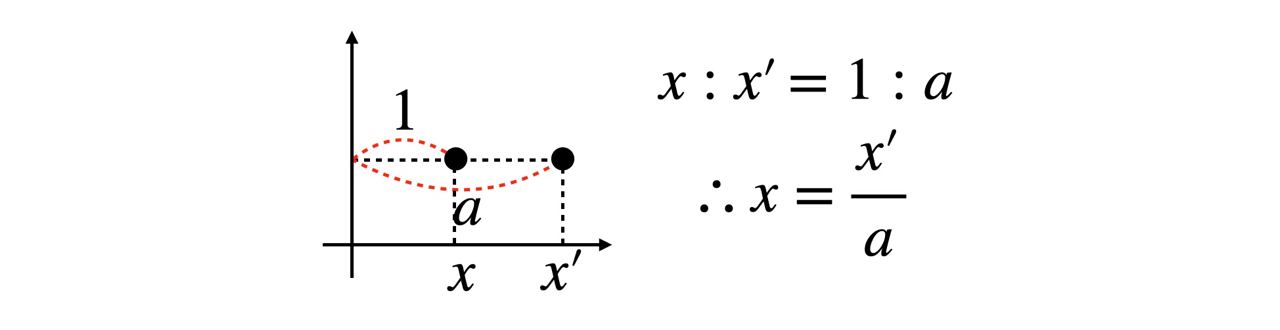
마찬가지로 단위원 위의 임의의 점의 두 번째 좌표값인 $y$를 수직축 방향으로 $b$배 확대한 새로운 값 $y\prime{}$은 $y$와 다음과 같은 관계를 가짐을 알 수 있다.
$y = \frac{y\prime{}}{b}$
그런데 $x^2 + y^2 = 1$이므로, 이 식에 $x = \frac{x\prime{}}{a}$와 $y = \frac{y\prime{}}{b}$를 대입하면 타원의 방정식인 $\frac{x\prime{}^2}{a^2} + \frac{y\prime{}^2}{b^2} = 1$을 얻을 수 있다.
즉, 중심이 원점에 있고 반지름인 1인 단위원을 $x$축으로 $a$ 만큼, $y$축으로 $b$ 만큼 확대(또는 축소)한 도형은 타원임을 알 수 있다.
따라서 타원 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$의 그래프는 다음과 같이 그릴 수 있다.