Sphere: Area and Volume

Finding the surface area and volume of a sphere without using integrals

본 포스트에는 수식이 포함되어 있습니다. 분수 등의 수식이 정상적으로 보이지 않는 경우에는 수식을 마우스 오른쪽 버튼으로 클릭한 후 “Math Renderer”를 SVG로 바꿔주세요. (➔How-To)

반지름이 $r$인 구(sphere)의 겉넓이와 부피를 계산하는 공식은 각각 다음과 같다.

$\text{area} = 4 \pi r^2 \;\;\; \text{volume} = \frac{4}{3} \pi r^3$

적분을 이용하면 간단명료하게 위의 두 가지 공식을 증명할 수 있다. (구글이나 유튜브에서 검색해 보면 관련 내용을 쉽게 찾아볼 수 있다.)

하지만 문제는 중학교 1학년 수학 교과서에 구의 겉넓이와 부피 공식이 등장한다는 것이다. 많은 학생들이 선행학습을 한다고는 하지만 고등학교 2학년 교과과정에서야 배우는 적분을 활용하여 이 공식을 증명하는 것은 분명 문제가 있다.

그래서 중학교 수학에서는 이를 어떻게 설명하는지 첫째 아이의 교과서 및 문제집을 살펴보았다. 일반적인 중학교 교과서 및 문제집에서 구의 겉넓이와 부피를 설명하는 방식은 다음과 같다.

[구의 겉넓이]

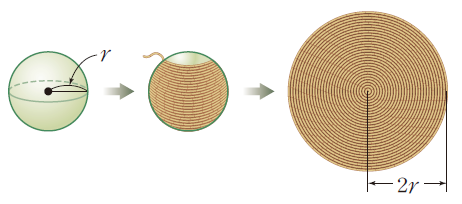
구의 겉면을 노끈으로 빈틈 없이 겹치지 않게 감는다. 이 노끈을 풀어서 평면 위에 납작한 원을 만들면 반지름의 길이가 $2r$이 된다. 즉, 반지름의 길이가 $r$인 구의 겉넓이는 반지름의 길이가 $2r$인 원의 넓이와 같다.

[구의 부피]

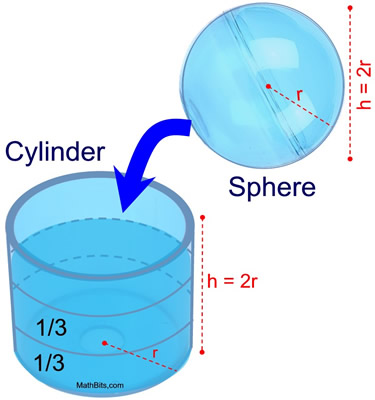
밑면인 원의 반지름이 $r$, 높이가 $2r$인 원기둥 모양의 그릇에 물을 가득 채운다. 이 그릇에 반지름이 $r$인 구를 넣었다 빼면 원기둥 높이의 $\frac{1}{3}$ 만큼의 물이 남는다. 즉, 원기둥 높이의 $\frac{2}{3}$에 해당하는 물이 넘친다. 넘친 물의 부피는 우리가 구하고자 하는 구의 부피와 같기 때문에 구의 부피는 원기둥 부피의 $\frac{2}{3}$가 된다.

나름 중학교 1학년 수준에 맞는 정도에서 최대한 직관적으로 구의 겉넓이와 부피 공식의 의미를 설명하려고 하는 것 같다. (사실 직관적이라는 부분도 동의하기 어렵다.) 하지만 위의 내용들은 수학적으로 엄밀한 증명이라고 보기는 어렵다. 공식이 어떻게 만들어 졌는지에 대한 이유라기 보다는 오히려 결과에 가깝기 때문이다.

“일단 중요하니 대략의 의미를 이해하고 결과를 외워라! 엄밀한 증명은 몇 년 뒤에 적분을 배우면 알려주겠다.” 정도의 전략으로 보인다.

“구의 겉넓이: 4 파이 알 제곱”

“구의 부피: 3분의 4 파이 알 세제곱”

이 공식들은 매우 중요하기 때문에 반드시 암기를 해야 한다. 하지만 공식의 암기로 그치기에는 무언가 석연치 않고 찜찜함을 느끼는 사람들이 있을 수 있다. 이 공식이 어떻게 만들어졌는지에 대한 지적 호기심을 가지고 있거나, 또는 진짜 맞는 식인지에 대한 의심이 드는 사람들은 수학적인 증명의 필요성을 느낄 것이다. 그리고, 단순히 저 공식들을 외워서 문제를 기계적으로 푸는 것 보다는 공식이 생겨난 과정을 이해하는 것이 훨씬 더 좋은 접근법인 것임은 분명하다.

그렇다면 적분을 사용하지 않고서도 구의 겉넓이와 부피 공식을 유도할 수 있을까? 평상시에 생각해보지 못한 문제였다. 결론은 “할 수 있다!”이다. 구글과 유튜브를 통해 관련 자료들을 찾아보았고 그 결과를 최대한 간단하게 정리해보았다. (즉, 이제부터가 본론이다.)

구의 겉넓이 공식을 유도해보자.

그 전에 먼저 알아야할 내용이 있다.

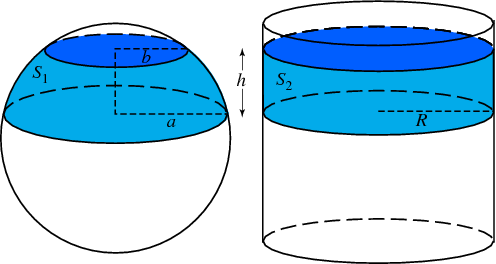
위의 그림에서 $S_1$과 $S_2$의 넓이가 같다는 사실을 아르키메데스의 모자상자 정리(Archimedes’ HatBox Theorem)라고 한다.

이 정리에 의하여 $h = 2r$이 되면 다음의 등식이 성립한다.

구의 겉넓이 = 원기둥의 옆면의 넓이

원기둥의 옆면을 잘라서 펼치면 다음과 같은 직사각형이 된다. 이 직사각형의 밑변의 길이는 반지름이 $r$인 원의 둘레의 길이이고, 높이는 반지름의 두 배인 $2r$이다.

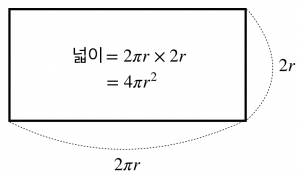
“구의 겉넓이: 4 파이 알 제곱”임이 증명되었다! Q.E.D.

참고로 “구의 겉넓이 = 원기둥의 옆면의 넓이”가 되는 것을 진짜 털실을 가지고 확인해본 유튜버가 있다. 관심 있는 분들은 아래의 링크에서 내용을 확인해 보시라. 링크

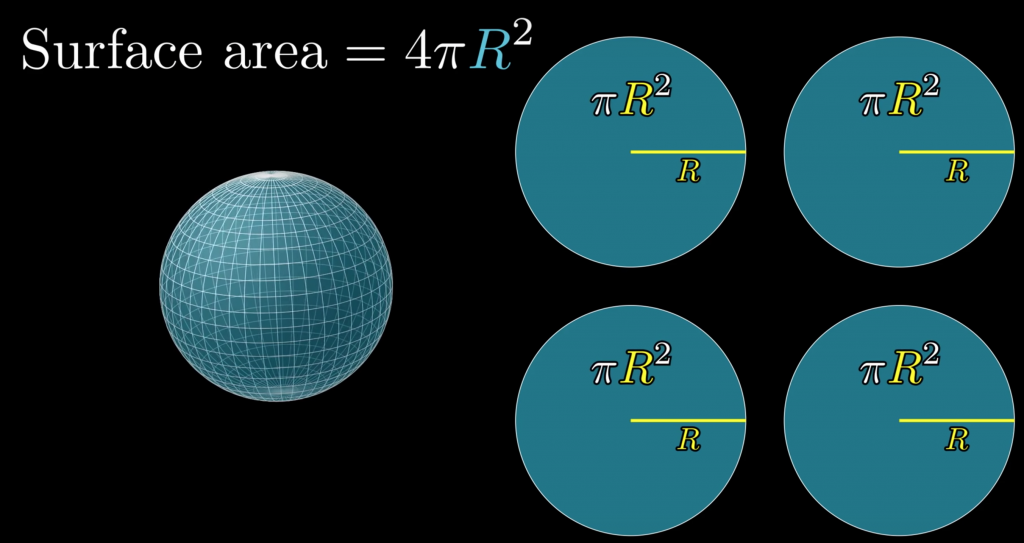
여기서 잠깐. 한 가지 특이한 사실을 확인하고 다음으로 넘어가자. 구의 겉넓이는 구의 중심을 지나는 평면으로 구를 잘랐을 때 만들어지는 원의 넓이의 4배이다.

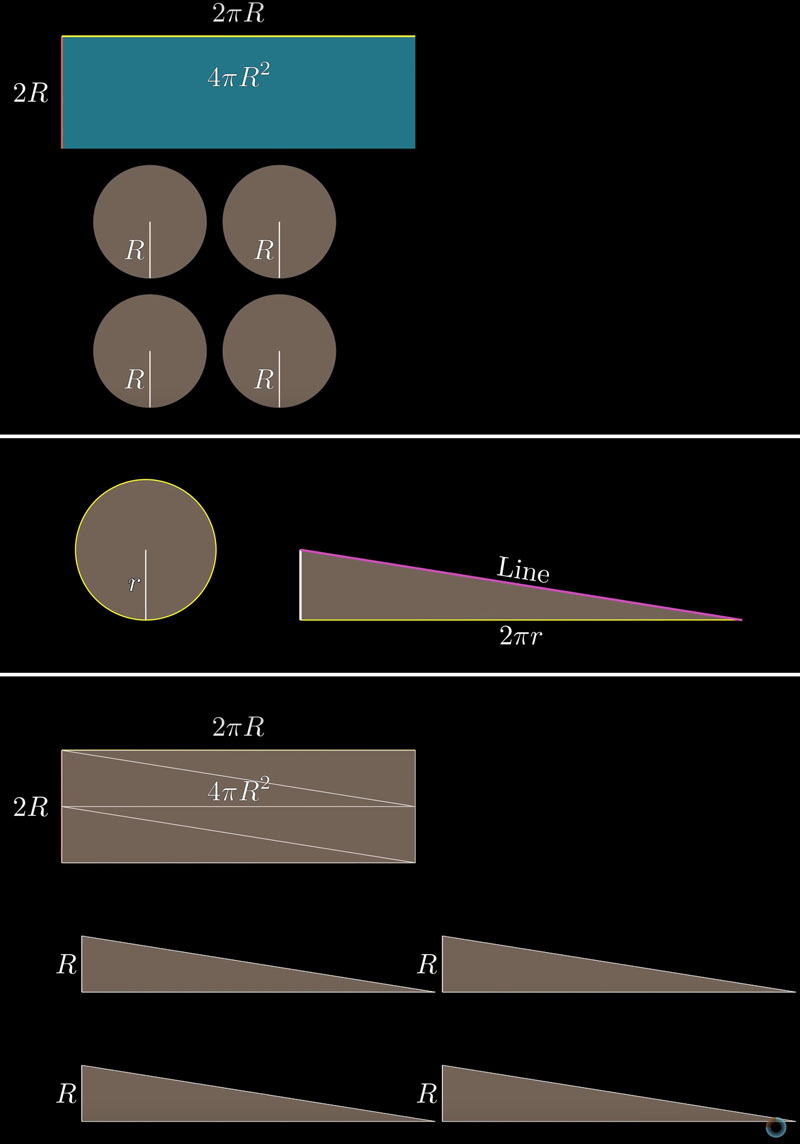
이제 구의 부피를 구해보자. 구의 부피는 구의 겉넓이를 이용하여 계산한다.

다음 그림과 같이 구를 $n$개의 각뿔들의 합으로 생각할 수 있다. (삼각뿔이어도 상관 없고 사각뿔, 오각뿔이어도 상관없다. 심지어 여러 모양의 각뿔들이 섞여 있어도 된다.)

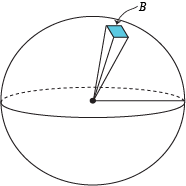
각 각뿔들의 밑면의 모양과 넓이는 다를 수 있지만 높이는 모두 구의 반지름인 $r$로 동일하다. 각 각뿔들의 밑면의 넓이를 각각 $B_1$, $B_2$, $\cdots$, $B_n$이라고 하자. (여기서 $n$은 매우 큰 수이다. $n$이 크면 클수록 구의 부피에 수렴한다.) 이때 모든 각뿔들의 부피를 더하면 구의 부피가 되므로 다음과 같은 식이 성립한다. (이 글을 읽는 사람들은 각뿔의 부피는 각기둥의 부피의 $\frac{1}{3}$이라는 사실을 알고 있다고 가정한다. 이에 대한 수학적 증명은 초등수학을 결정하는 개념 총정리라는 책에 정리되어 있다.)

따라서 구의 부피는 다음과 같다.

보다 자세한 설명은 다음 링크에서 확인할 수 있다. Q.E.D.

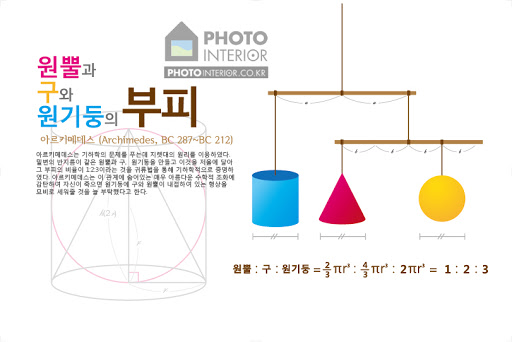
마지막으로 한 가지 중요한 사실을 확인해보자. 다음 그림과 같이 반지름을 공유하는 원뿔, 원기둥, 구의 부피 사이에는 1:2:3의 비가 성립한다.

아르키메데스는 이러한 사실을 알고 있었고, 이를 이용하여 원기둥의 부피로부터 구의 부피를 계산하였다고 한다.

그리고, 아르키메데스의 묘비에는 이 그림이 새겨져 있었다고 한다. 따라서, 이 그림을 “아르키메데스의 묘비 (Archimedes’ tombstone)” 그림이라고 부른다.