Archimedes’ HatBox Theorem

Relationship between the surface area of ​​a sphere and a cylinder

본 포스트에는 수식이 포함되어 있습니다. 분수 등의 수식이 정상적으로 보이지 않는 경우에는 수식을 마우스 오른쪽 버튼으로 클릭한 후 “Math Renderer”를 SVG로 바꿔주세요. (➔How-To)

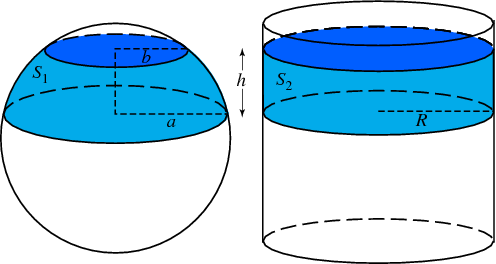
위의 그림에서 $S_1$과 $S_2$의 넓이가 같다는 사실을 아르키메데스의 모자상자 정리(Archimedes’ HatBox Theorem)라고 한다. 그 이유를 대략적으로 살펴보면 다음과 같다.

높이 $h$가 고정된 상태에서 이 높이가 나타내는 영역이 위 또는 아래로 움직이는 경우를 생각해보자. 원기둥의 경우 띠의 위치가 올라가거나 내려가더라도 $S_2$의 넓이는 변하지 않는다. 그런데 구의 경우 띠가 위로 올라갈수록 $S_1$은 점점 더 기울어지기 때문에 넓이가 증가하는 것처럼 보인다. 하지만 기울어져서 넓이가 증가하는 만큼 이에 정확하게 비례해서 반지름이 감소하면서 기울기 변화에 의한 넓이 증가분을 상쇄시키기 때문에 넓이는 변하지 않는다.

수학적으로 보다 엄밀하게 증명을 해보자.

다음 그림과 같이 구 표면을 사각형으로 잘게 쪼개보자. (북극과 남극 주변은 삼각형이지만 사각형의 특수한 경우로 볼 수 있기 때문에 문제가 되지 않는다.)

같은 위도상(여기서는 위에서 5번째 줄)에 존재하는 띠 형태를 구성하는 사각형 요소들을 합하면 위의 그림에서의 $S_1$이 된다. 임의의 $S_1$에 속해 있는 사각형 요소들 중에서 하나를 선택해서 생각해보자. 이 사각형 요소를 노란색으로 표시하였다. 수직 방향의 중심축에서 바깥쪽 방향으로 뻗어 나와서 원기둥 상에 투영(projection)되어 대응되는 사각형 또한 같은 노란색으로 표시하였다. (이 사각형은 $S_2$를 구성하는 요소이다.) 이 때 해당 요소들만을 떼어내서 생각하면 다음과 같은 쐐기(wedge) 형태가 된다.

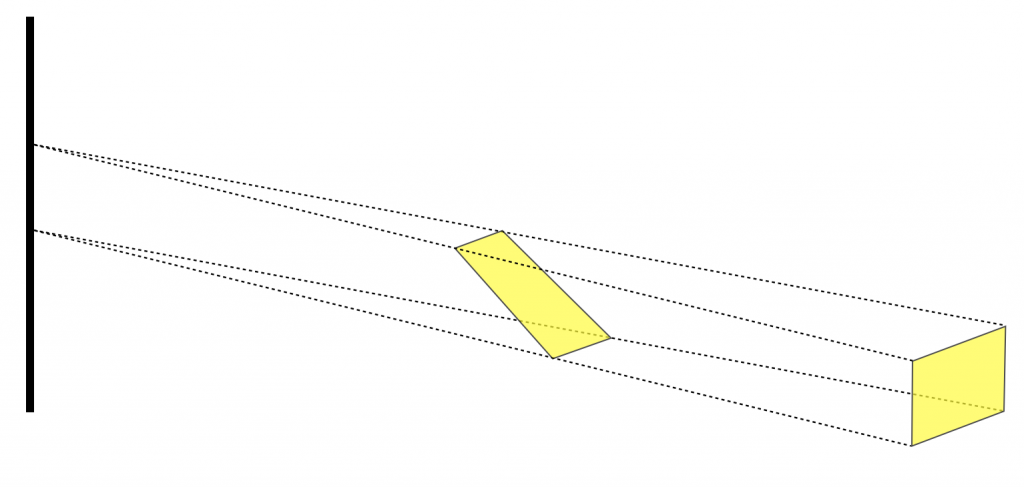
그림상에서는 둘 다 곡면상에 존재하기 때문에 직사각형이 아니지만 높이 $h$를 무한히 작게 만들면 곡면은 평면으로 수렴되고, 이 평면상에 존재하는 도형은 직사각형으로 간주할 수 있다.

결론부터 말하면 이 두 직사각형의 넓이가 같고, 다른 직사각형 요소들에 대해서도 이 내용이 성립하기 때문에 $S_1$의 넓이와 $S_2$의 넓이가 같다는 것이다.

두 직사각형의 넓이가 같음을 증명해보자.

구(sphere) 상에 존재하는 직사각형을 빨간색으로 표시하고 밑변의 길이와 높이를 각각 $x$와 $y$라 하자. 마찬가지로 원기둥(cylinder) 상에 존재하는 직사각형을 파란색으로 표시하고 밑변의 길이와 높이를 각각 $w$와 $h$라고 하자.

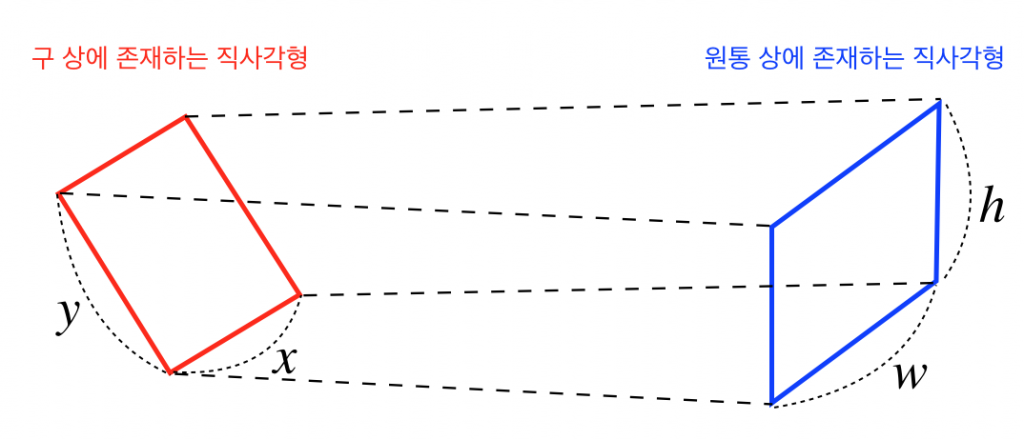
위의 그림은 구를 옆에서 본 모습이다. 편의상 빨간색 직사각형과 파란색 직사각형을 크게 그렸지만 사실 이 두 사각형의 크기는 굉장히 작다는 것을 명심해야 한다.

위의 그림에서 $d$는 $0$ ~ $r$ 사이의 값을 가진다. 즉, 띠가 북극 또는 남극에 위치할 때 $d=0$이고, 적도에 위치할 때 $d=r$이 된다.

이 그림을 위에서 보면 다음과 같이 보인다.

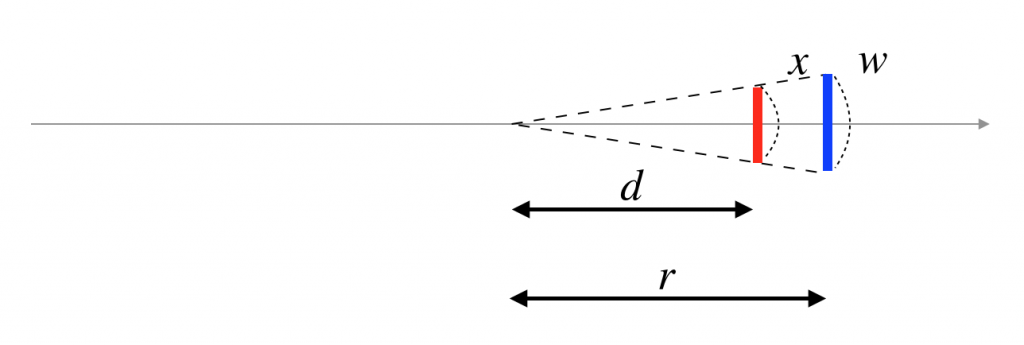
빨간색을 밑변으로 가지는 이등변 삼각형과 파란색을 밑변으로 가지는 이등변 삼각형은 서로 닮음이다. 따라서, 다음과 같은 관계가 성립한다.

$d:r=x:w \;\;\; \Longrightarrow \;\;\; w=\frac{r}{d}x$

다시 옆에서 본 모양을 상상해보자.

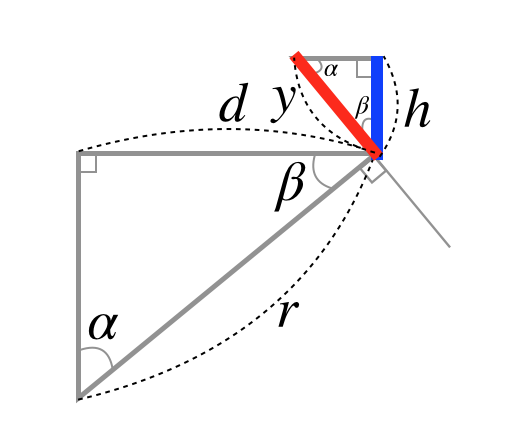
위의 그림에서 두 개의 직삼각형은 서로 닮음이다. 따라서, 다음과 같은 관계가 성립한다.

$d:r=h:y \;\;\; \Longrightarrow \;\;\; h=\frac{d}{r}y$

$\therefore w \times h = \frac{r}{d}x \times \frac{d}{r}y = x \times y$

$wh = xy$이기 때문에 두 노란색 사각형의 넓이가 같음이 확인되었다. 따라서, 아르키메데스의 모자상자 정리(Archimedes’ HatBox Theorem)가 성립한다는 것이 증명되었다. Q.E.D.