on
Newell’s Method
Fast Polygon Normal Calculation
본 포스트에는 수식이 포함되어 있습니다. 분수 등의 수식이 정상적으로 보이지 않는 경우에는 수식을 마우스 오른쪽 버튼으로 클릭한 후 “Math Renderer”를 SVG로 바꿔주세요. (➔How-To)
뉴웰 방법(Newell’s method)은 3차원 공간에서 다각형(polygon)의 법선 벡터(normal vector)를 구하는 방법입니다. 이 방법에 따르면, 다음 그림과 같이 네 점 $\mathbf{P}_1$, $\mathbf{P}_2$, $\mathbf{P}_3$, $\mathbf{P}_4$로 구성된 사각형이 있을 때, 이 사각형의 법선 벡터 $\overrightarrow{\mathbf{N}}$의 각 성분은 오른쪽 수식과 같이 계산할 수 있습니다.
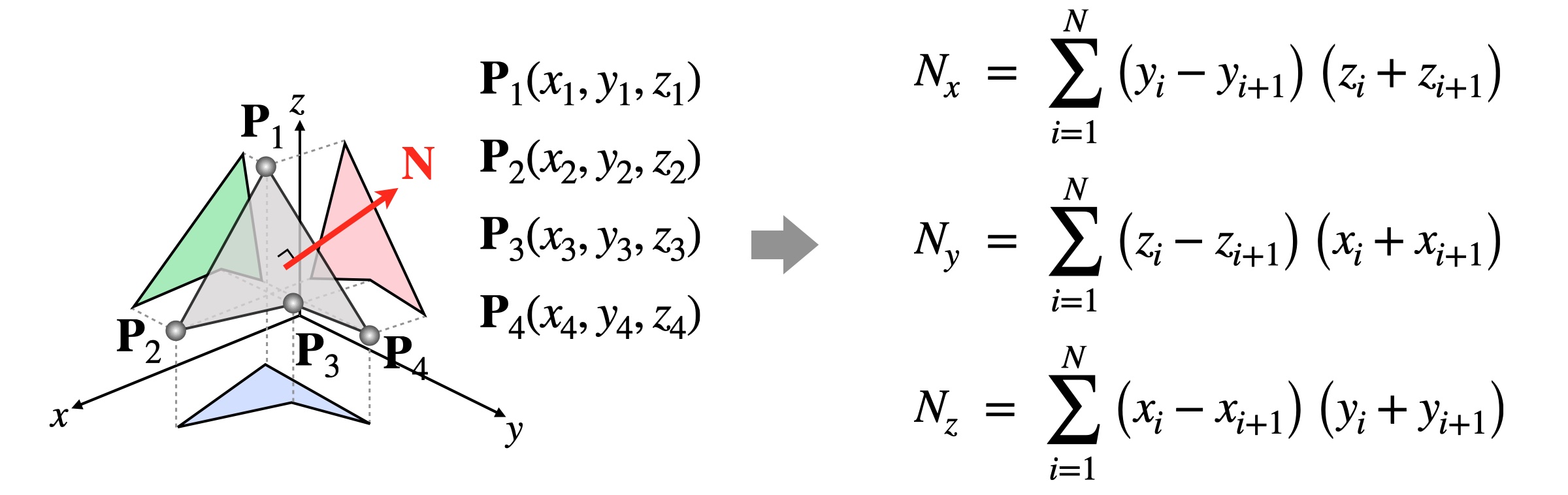
이 예에서 $N=4$이고, 마지막 점의 좌표는 처음 점의 좌표와 같다고 간주합니다. 즉, $(x_{N+1},y_{N+1},z_{N+1})=(x_{1},y_{1},z_{1})$라고 설정합니다.
3차원 공간에서 평평한 도형이 있을 때, 이 도형을 3개의 2차원 평면($xy$-평면, $yz$-평면, $zx$-평면)에 그림자처럼 투영한 넓이는 해당 도형의 법선 벡터와 밀접한 관련이 있습니다. 예를 들어, 이 도형이 $xy$-평면과 평행하다면, $yz$-평면과 $zx$-평면에 나타나는 그림자의 넓이는 0이 됩니다. 반면, $xy$-평면에 나타나는 그림자의 넓이는 원래 도형의 넓이와 같습니다. 이러한 투영된 넓이의 크기는 법선 벡터의 각 성분의 크기와 연관되어 있으며, 이 예에서는 $x$방향과 $y$방향 성분이 0이고 $z$방향 성분은 0이 아닌 값을 가져야 하므로, 법선 벡터는 $z$-축 방향임을 알 수 있습니다.
즉, 주어진 다각형의 법선 벡터는 다음과 같이 계산할 수 있습니다.
$\overrightarrow{\mathbf{M}}=(A_{yz},A_{zx}, A_{xy})\;\;\;\Longrightarrow\;\;\;\overrightarrow{\mathbf{N}}=\frac{\overrightarrow{\mathbf{M}}}{\Vert \overrightarrow{\mathbf{M}} \Vert}$
여기서 $A_{yz}$, $A_{zx}$, $A_{xy}$는 각각 주어진 다각형의 넓이 $A$를 $yz$-평면, $zx$-평면, $xy$-평면으로 투영한 넓이를 의미합니다.
왜 이렇게 투영한 넓이를 이용하여 법선 벡터를 나타낼 수 있는지 조금 더 수학적으로 엄밀히 살펴보겠습니다. 다음처럼 $xy$-평면과 $\theta$만큼의 각도를 이루고 있는 평면을 옆에서 보고 있다고 가정해 보겠습니다.

주어진 평면의 넓이를 $A$라 하고, 이 평면을 $xy$-평면에 투영한 넓이를 $A_{xy}$라 하면, 코사인 함수의 정의에 따라 $A_{xy}=A\cos\theta$와 같은 관계식이 성립합니다. 그리고 위의 그림에서 나타나는 모든 직각삼각형은 서로 닮음이라는 것과, 법선 벡터의 크기는 1이라는 사실로부터, 법선 벡터 $\overrightarrow{\mathbf{N}}$의 $z$-축 성분의 크기는 $N_z=\cos\theta$가 됨을 알 수 있습니다. 이 두 식에서 공통 부분인 $\cos\theta$를 정리해서 없애면 $N_z=\frac{A_{xy}}{A}$라는 결론을 얻을 수 있습니다. 마찬가지 방법으로, $x$-축 성분과 $y$-축 성분을 구해서 정리하면 법선 벡터 $\overrightarrow{\mathbf{N}}$은 다음과 같이 쓸 수 있습니다.
$\overrightarrow{\mathbf{N}}=(\frac{A_{yz}}{A},\frac{A_{zx}}{A},\frac{A_{xy}}{A})=\frac{1}{A}(A_{yz},A_{zx},A_{xy})$
그러므로 각 평면으로 투영한 넓이를 각각의 성분으로 가지는 벡터는 법선 벡터와 같은 방향을 나타냅니다.
이제 각 평면으로 투영된 다각형의 넓이를 구해보겠습니다. 2차원 평면상에 존재하는 임의의 다각형은 몇 개의 삼각형으로 분할된다는 사실과, 이때 각 삼각형의 크기는 삼각형을 구성하는 두 벡터의 외적으로 구한 벡터의 길이의 절반이 된다는 사실을 우리는 이미 알고 있습니다. 다만 외적을 구할 때 두 벡터의 순서에 따라서 부호를 결정할 수 있는데, 반시계 방향으로 외적한 결과 벡터의 길이로 구한 넓이를 양(+)의 부호를 가지도록 정의하고, 시계 방향으로 외적한 결과 벡터의 길이로 구한 넓이를 음(-)의 부호를 가지도록 정의하겠습니다. 이렇게 외적의 순서에 따라서 양과 음의 부호를 모두 가질 수 있도록 정의한 넓이를 부호 넓이(signed area)라고 합니다.
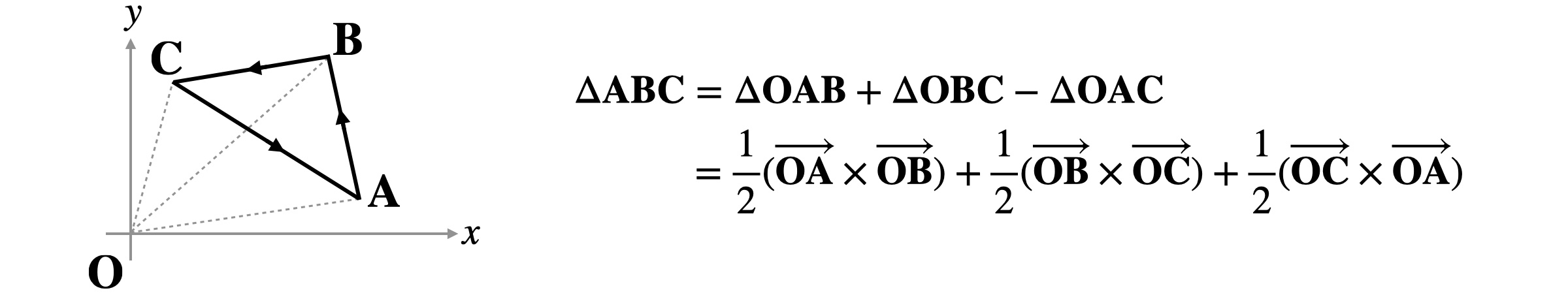
부호 넓이에 대한 한 가지 예를 살펴보겠습니다. 다음과 같이 $xy$-평면상에 존재하는 2차원 삼각형 ABC가 있다고 가정하겠습니다. 그러면 이 삼각형의 넓이는 부호 넓이를 이용하여 다음과 같이 계산할 수 있습니다.
하나의 $n$각형은 $n-1$개의 삼각형의 합으로 구성됩니다. 따라서 $N$개의 정점 $V_i$로 구성되는 다각형의 넓이는 다음과 같은 공식으로 확장될 수 있습니다. (단, $i$ = 1, 2, $\cdots$, $N$)
$\frac{1}{2} \sum_{i=1}^{N} ( \overrightarrow{\mathbf{OV}}_i \times \overrightarrow{\mathbf{OV}}_{next(i)} )$
단, 여기서 $next(i)$는 일반적으로 $i$번째 정점의 다음 정점인 $i+1$번째 정점의 인덱스를 의미하고, 마지막 인덱스 $i=N$일 때는 다음 점인 $N+1$번째 점이 존재하지 않기 때문에 다시 처음 점인 첫 번째 점의 인덱스 $i=0$을 출력으로 뱉어주는 함수입니다.
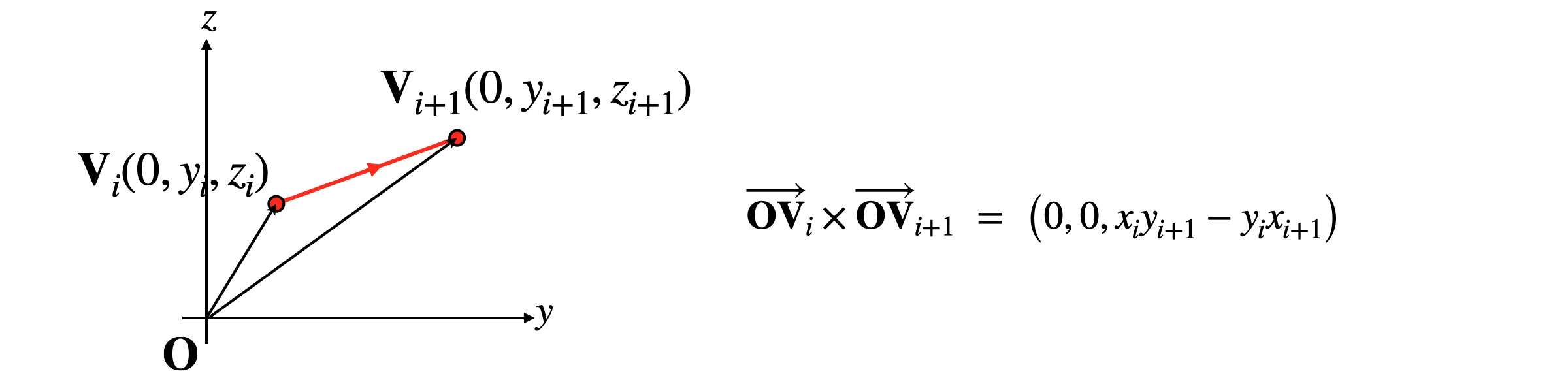
세 점 $O_{}$, $V_{i}$, $V_{i+1}$로 구성되는 삼각형의 넓이는 다음과 같습니다.
$x_i y_{i+1} - y_i x_{i+1}$
따라서 $N$개의 점 $V_{i}, V_{2}, \cdots ,V_{N}$으로 구성되는 다각형의 넓이는 다음과 같습니다.
$(x_1 y_2 - y_1 x_2) + (x_2 y_3 - y_2 x_3) + \cdots + (x_N y_1 - y_N x_1)$
$=(x_1 y_1 + x_1 y_2 - y_1 x_2 - x_2 y_2) + (x_2 y_2 + x_2 y_3 - y_2 x_3 - x_3 y_3) + \cdots + (x_{N-1} y_{N-1} + x_N y_1 - y_N x_1 - x_1 y_1)$
$=(x_1 - x_2) (y_1 + y_2) + (x_2 - x_3) (y_2 + y_3) + \cdots + (x_N - x_1) (y_N + y_1)$
$= \sum_{i=1}^N (x_i - x_{next(i)}) (y_i + y_{next(i)})$
이것은 주어진 3차원 다각형을 $yz$-평면으로 투영한 넓이를 구한 것입니다. 마찬가지로 주어진 3차원 다각형을 $zx$-평면과 $xy$-평면으로 각각 투영한 넓이를 구하여 정리하면 이 다각형의 법선 벡터를 다음과 같이 구할 수 있습니다.
$\overrightarrow{\mathbf{M}}=(A_{yz},A_{zx},A_{xy})$
$\overrightarrow{\mathbf{N}}=\frac{\overrightarrow{\mathbf{M}}}{\Vert \overrightarrow{\mathbf{M}} \Vert}$
$A_{yz}=\sum_{i=1}^N(y_i - y_{i+1})(z_i + z_{i+1})$
$A_{zx}=\sum_{i=1}^N(z_i - z_{i+1})(x_i + x_{i+1})$
$A_{xy}=\sum_{i=1}^N(x_i - x_{i+1})(y_i + y_{i+1})$
Q.E.D.