Written by wano
on 

Prism & Pyramid

The reason why the volume of a pyramid is one-third of that of a prism

본 포스트에는 수식이 포함되어 있습니다. 분수 등의 수식이 정상적으로 보이지 않는 경우에는 수식을 마우스 오른쪽 버튼으로 클릭한 후 “Math Renderer”를 SVG로 바꿔주세요. (➔How-To)

다각기둥과 다각뿔의 부피 관계는 삼각기둥과 삼각뿔의 부피 관계를 고찰하면 됩니다. 왜냐하면, 다각기둥의 밑면은 여러 개의 삼각형으로 분할할 수 있기 때문입니다.

삼각기둥의 부피와 삼각뿔의 부피 사이에는 다음과 같은 관계식이 성립합니다.

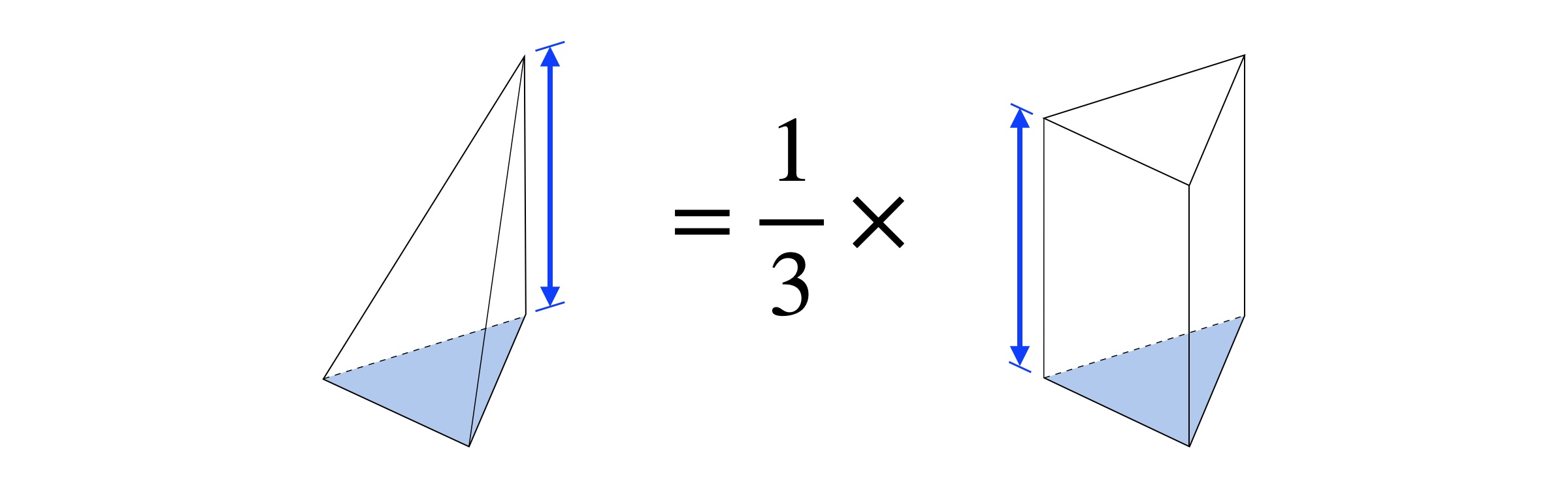
$V_{prism} = \frac{1}{3} V_{pyramid}$

여기서 1/3이라는 수가 어떻게 나왔는지는, 정적분을 이용하면 깔끔하게 증명할 수 있습니다. 하지만 여기서는 적분을 사용하지 않고 증명을 해보겠습니다.

우선, 형태가 다르더라도 밑면의 넓이와 높이가 같으면 두 사각뿔의 부피는 동일합니다.

이것은 다음 그림과 같이 사각뿔을 잘게 슬라이스(slice) 내어서 수평방향으로 이동한 결과이기 때문이라고 직관적으로 이해할 수도 있습니다.

이 원리는 밑변의 길이와 높이가 동일한 모든 삼각형의 넓이가 같다는 잘 알려진 사실을 부피로 확장한 개념이기도 합니다.

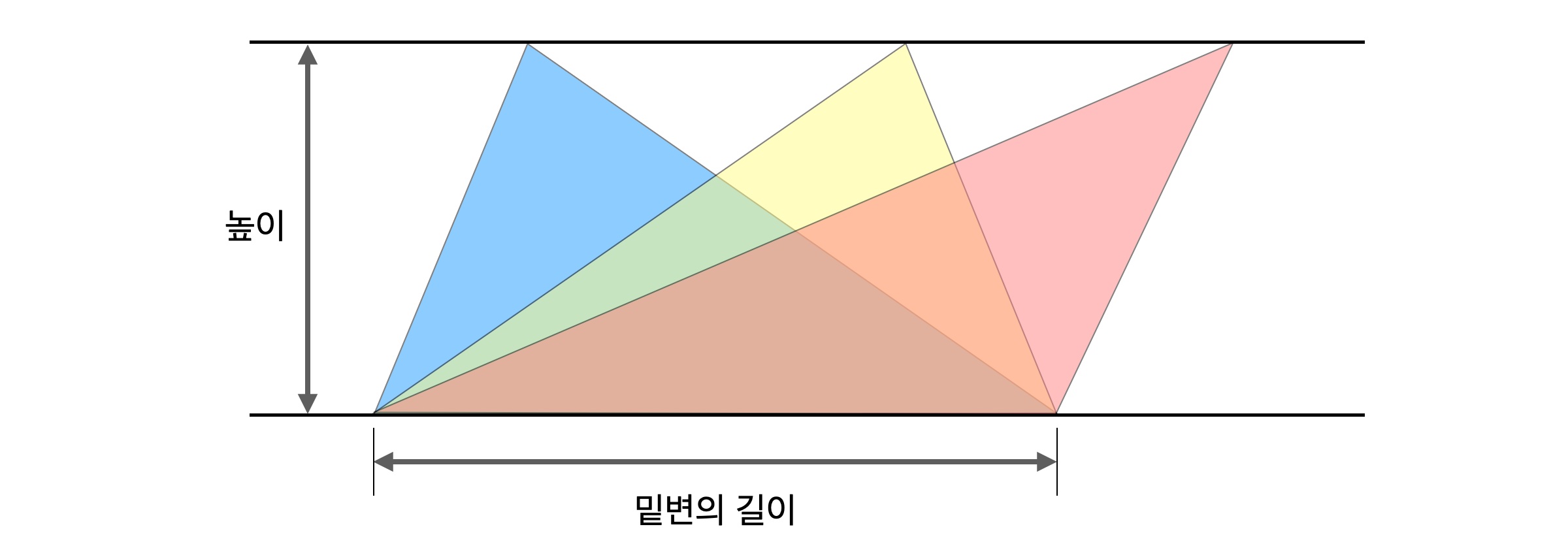
사각뿔과 마찬가지 이유로 밑면의 넓이와 높이가 동일한 두 삼각뿔의 부피는 같습니다.

한편, 다음 그림과 같이 삼각기둥(①)은 삼각쐐기(②)와 삼각뿔(③)로 분할할 수 있고, 삼각쐐기(②)는 다시 두 개의 삼각뿔(④와 ⑤)로 분할할 수 있습니다.

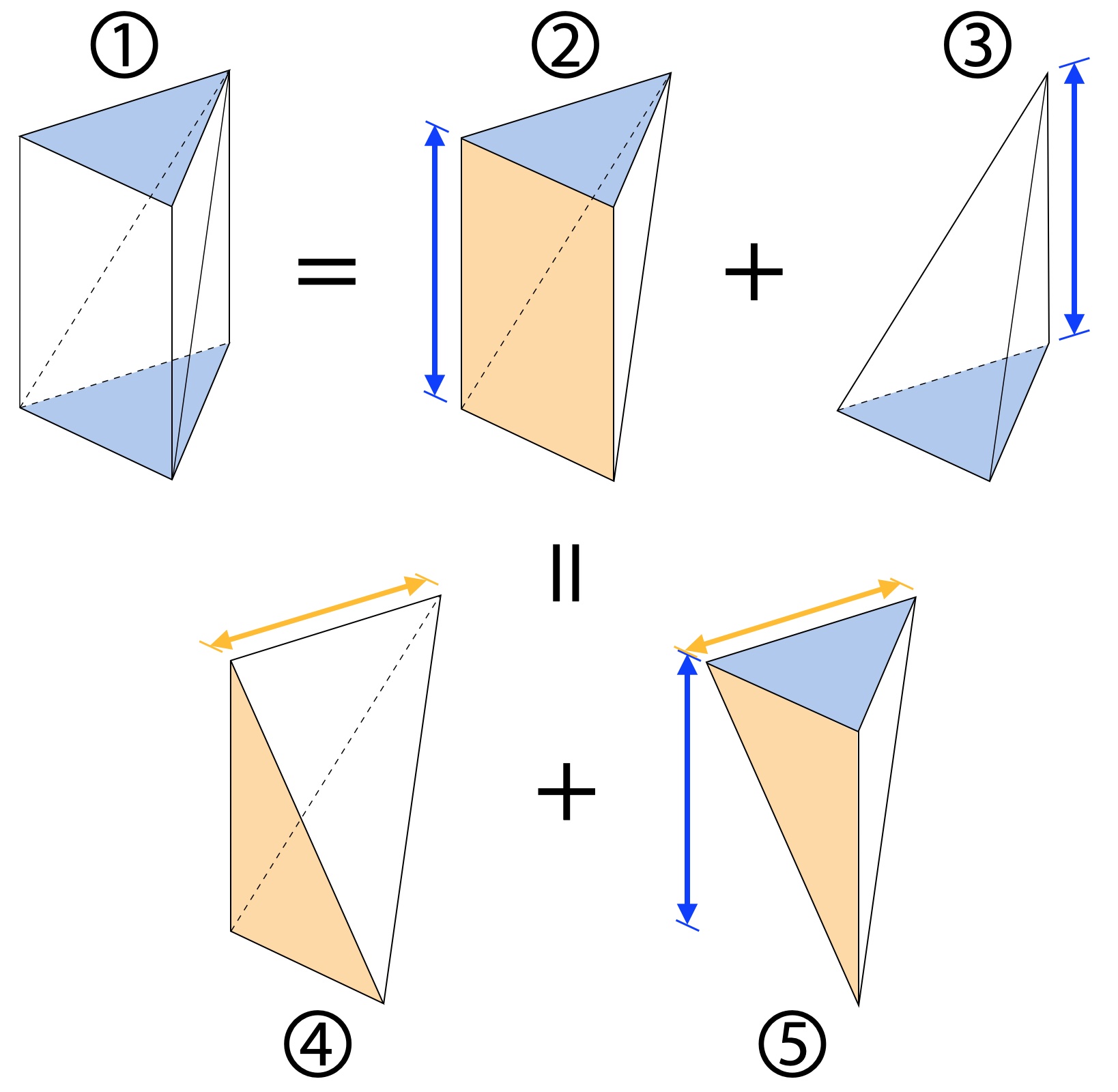
이때 다음과 같은 두 가지 사실이 성립합니다.

즉, ④=⑤ 이고 ③=⑤ 이기 때문에 세 삼각뿔 ③, ④, ⑤는 모두 부피가 같습니다.

따라서 다음과 같은 관계가 성립합니다.

③ = ④ = ⑤ = $\frac{1}{3} \times$ ①

이러한 관계는 사각기둥-사각뿔, 오각기둥-오각뿔, 육각기둥-육각뿔, … 의 경우에 대해서도 마찬가지로 성립합니다. 왜냐하면 임의의 다각뿔은 같은 높이를 가지는 $n$개의 삼각뿔로 분할할 수 있기 때문입니다.

그리고 이러한 사실은 원기둥-원뿔에도 동일하게 적용됩니다. 왜냐하면 원기둥과 원뿔은 각각 무한각기둥과 무한각뿔이라고 볼 수 있기 때문입니다. 따라서, 원뿔의 부피는 원기둥 부피의 3분의 1이 된다는 사실을 알 수 있습니다.