on
Pascal's Triangle
Pascal’s triangle is a triangular array of the binomial coefficients.
본 포스트에는 수식이 포함되어 있습니다. 분수 등의 수식이 정상적으로 보이지 않는 경우에는 수식을 마우스 오른쪽 버튼으로 클릭한 후 “Math Renderer”를 SVG로 바꿔주세요. (➔How-To)
다음과 같이 두 변수 $a$와 $b$로 이루어진 이항식(二項式, binomial = 항이 2개인 다항식)의 거듭제곱식을 전개하면 다음과 같다.
$(a+b)^2 = a^2 + 2ab + b^2$
$(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$
무언가 규칙이 있는 것처럼 보인다. 일반적인 자연수 $n(= 1, 2, 3, \cdots)$에 대한 $(a+b)^n$의 전개는 어떻게 될까?
$(a+b)^n$을 전개한 식의 $k$번째 항의 계수를 $_{n} C _{k-1}$라 하면 다음과 같이 쓸 수 있다.
$(a+b)^n = _{n} C _{0} a^n b^0 + _{n} C _{1} a^{n-1} b^1 + \cdots + _{n} C _{k-1} a^{n-k+1} b^{k-1} + _{n} C _{k} a^{n-k} b^k + \cdots + _{n} C _{n} a^0 b^n$
위의 식은 $a$에 대한 내림차순으로 정리한 식으로 $a^n b^0$항을 시작으로 $a$의 차수는 1씩 감소하고, $b$의 차수는 1씩 증가하여 총 $n+1$개의 항을 가지는 다항식이다. 이처럼 이항식의 거듭제곱을 일련의 단항식들의 합으로 전개하는 것을 이항정리(二項定理, binomial theorem)라고 한다.
여기서 $_{n} C _{k-1}$의 $C$는 계수(coefficient)의 약자로 사용되었지만 조합(combination)의 의미 또한 가진다. 이와 관련된 내용은 이항정리를 참고바란다.
한편 마찬가지 방법으로 차수가 하나 작은 $(a+b)^{n-1}$을 전개한 식의 $k$번째 항의 계수를 $_{n-1} C _{k-1}$라 할 수 있으므로 $(a+b)^{n-1}$을 전개하면 다음과 같다.
$(a+b)^{n-1} = _{n-1} C _{0} a^{n-1} b^0 + _{n-1} C _{1} a^{n-2} b^1 + \cdots + _{n-1} C _{k-1} a^{n-k} b^{k-1} + _{n-1} C _{k} a^{n-k-1} b^k + \cdots$
여기서 $a^{n-k-1} b^k$보다 뒤에 있는 항들은 중요하지 않으므로 생략하였다.
그런데 $(a+b)^n = (a+b)^{n-1} (a+b)$이므로 $(a+b)^n$의 $k+1$번째 항은 $(a+b)^{n-1}$의 $k$번째 항과 $k+1$ 항에 각각 $b$와 $a$를 곱해서 만들어지는 것을 알 수 있다.
$\cdots + _{n} C _{k} a^{n-k} b^{k} + \cdots = (\cdots + _{n-1} C _{k-1} a^{n-k} b^{k-1} + _{n-1} C _{k} a^{n-k-1} b^{k} + \cdots) \times (a+b)$
위의 식이 복잡하게 보이지만 사실 단순한 분배법칙을 적용한 것에 불과하기 때문에 천천히 따져보면 어렵지 않게 이해할 수 있다.
- $(a+b)^{n}$의 $k+1$번째 항: $_{n} C _{k} a^{n-k} b^{k}$
- $(a+b)^{n-1}$의 $k$번째 항: $_{n-1} C _{k-1} + a^{n-k} b^{k-1}$ (위의 1번 항과 비교하여 $b$의 차수가 하나 작음)
- $(a+b)^{n-1}$의 $k+1$번째 항: $_{n-1} C _{k} a^{n-k-1} b^{k}$ (위의 1번 항과 비교하여 $a$의 차수가 하나 작음)
즉, 2번 항의 계수와 3번 항의 계수가 합해져서 1번 항의 계수가 된다. 따라서 다음과 같은 사실이 성립합을 알 수 있다.
$\color{red}{_{n} C _{k} = _{n-1} C _{k-1} + _{n-1} C _{k}}$
위의 수식이 이번 포스팅의 핵심 내용이다.
이 등식을 3개의 6각형을 사용하여 도식화하면 다음과 같다.

이것을 모든 자연수 $n$과 $k$에 대해서 일반화하여 그리면 다음과 같다.
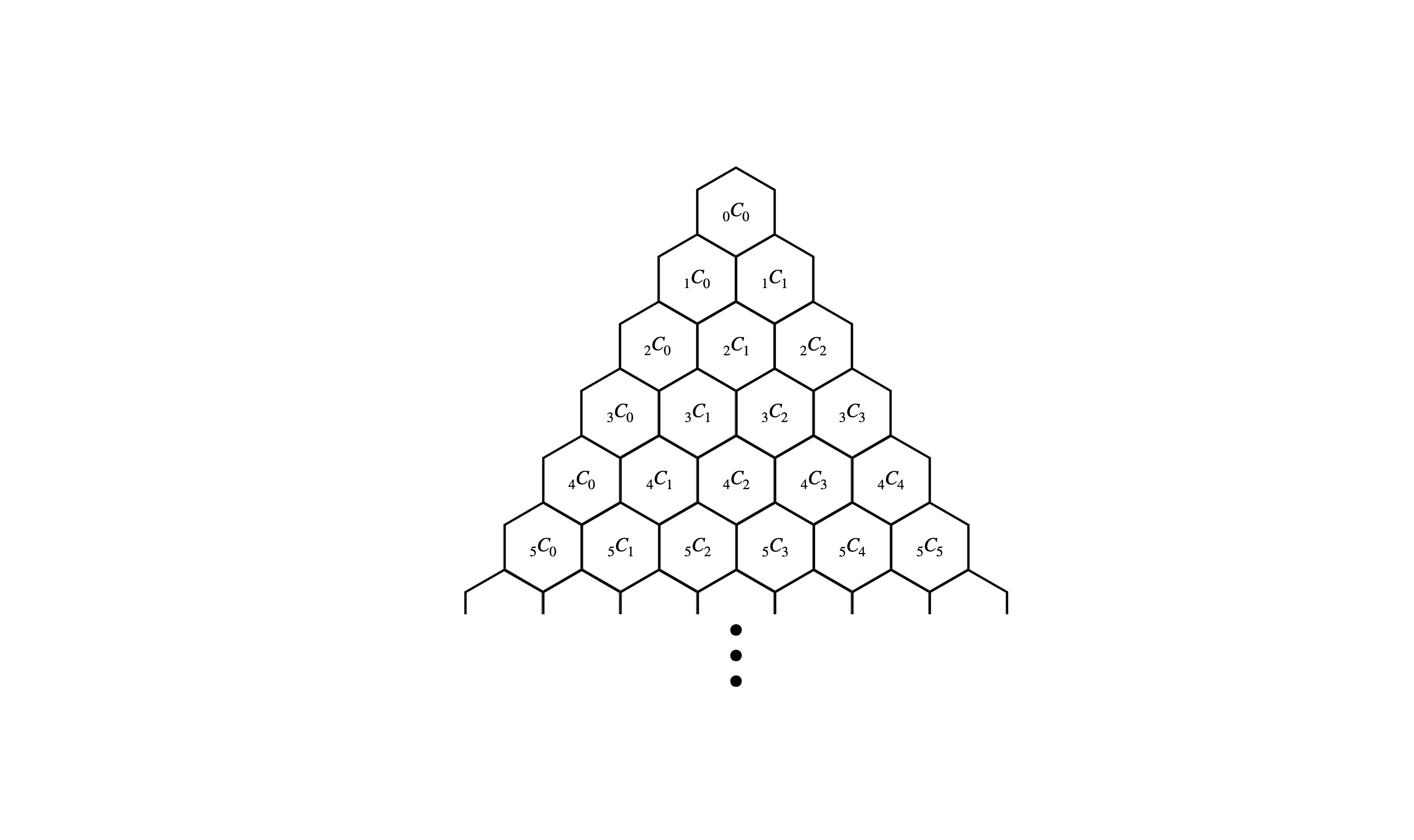
이러한 삼각형을 파스칼의 삼각형(Pascal’s Triangle)이라고 한다. 인도의 수학자들은 이것을 “메루산의 계단”이라는 이름으로 불렀고, 이란과 중국에서는 각각 “카얌 삼각형”과 “양휘의 삼각형”이라고 불렀으나, 후대에 프랑스의 수학자인 파스칼이 집대성하여 그의 이름이 붙여졌다고 한다.
임의의 수에 0을 더하면 원래의 수와 같기 때문에 파스칼의 삼각형은 다음과 같이 가상의 0으로 둘러싸인 개념으로 생각할 수도 있다.
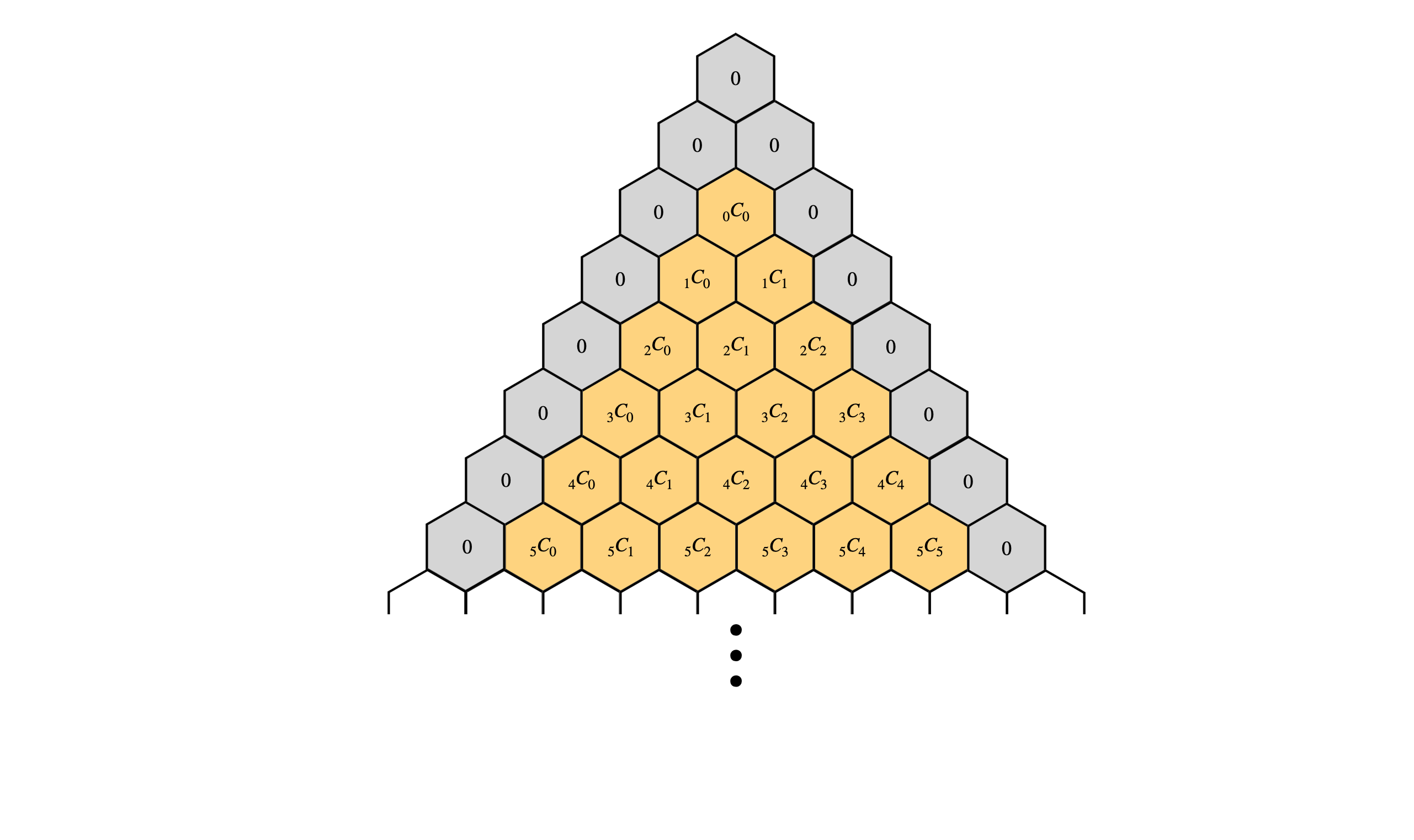
파스칼의 삼각형을 이용하면 이항식을 전개한 각 항의 계수를 쉽게 구할 수 있다. 각 행(row)의 숫자가 차례대로 $(a+b)^n$를 전개한 항의 계수이기 때문이다.
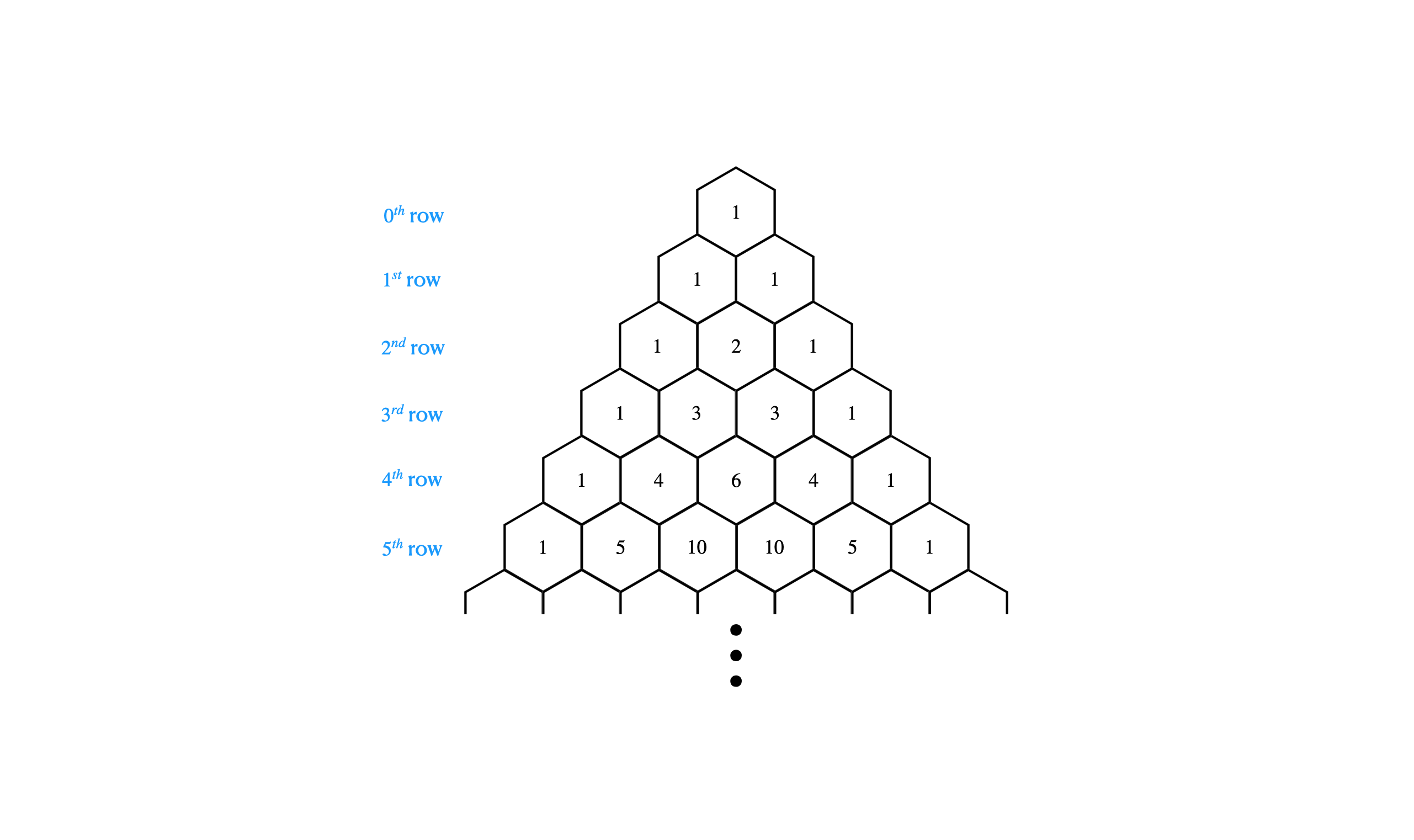
파스칼의 삼각형이 유명해진 이유는 이 외에도 여러 가지 신기한 성질들을 가지기 때문이다. 파스칼의 삼각형이 가지는 몇 가지 대표적인 패턴은 다음과 같다.
성질 1) 파스칼의 삼각형은 좌우대칭이다.
성질 2) 다음과 같은 위치의 숫자들을 순서대로 나열하면 자연수들의 집합이 된다.
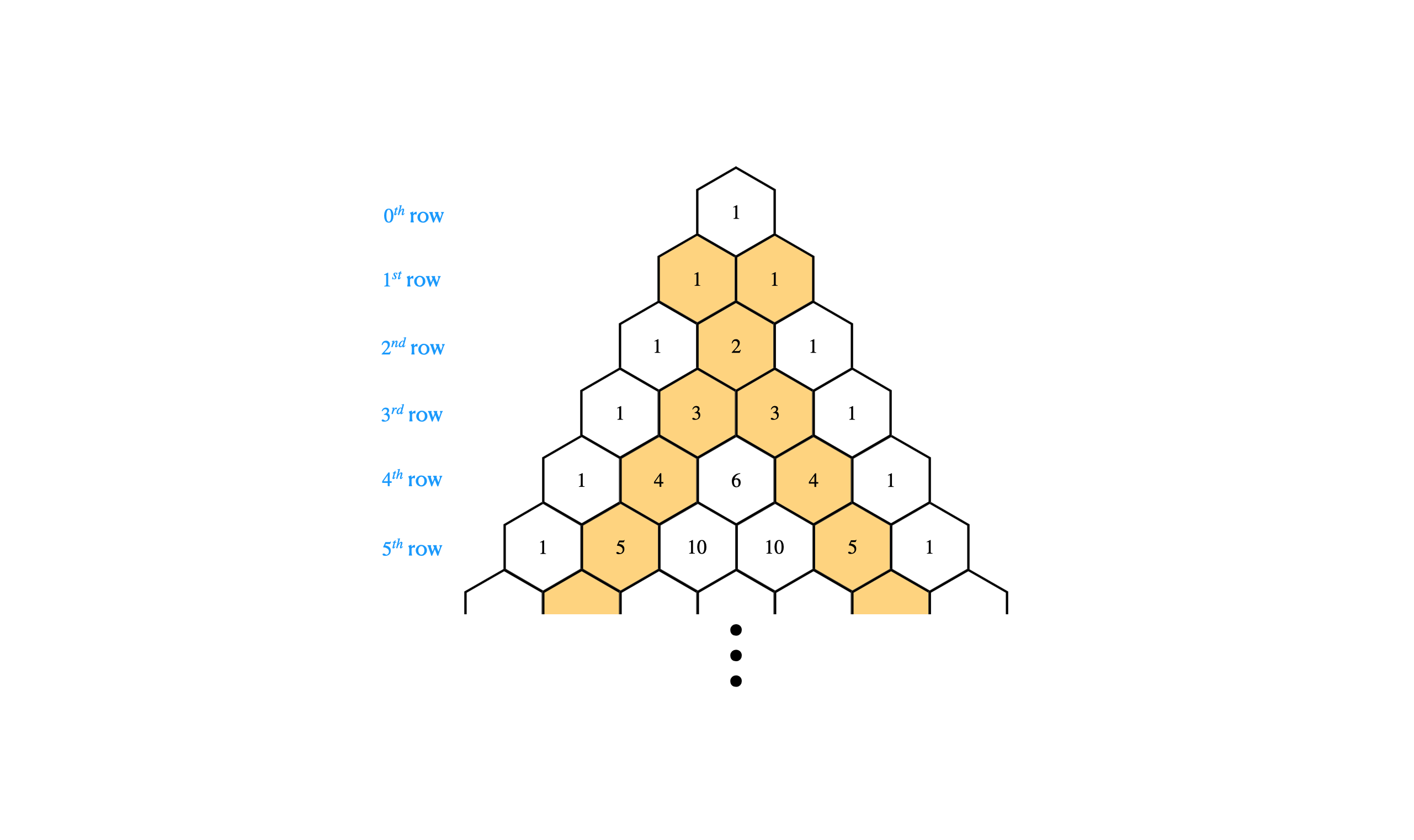
성질 3) 다음과 같은 위치의 숫자들은 정삼각형을 구성하는 점들의 개수를 의미한다.
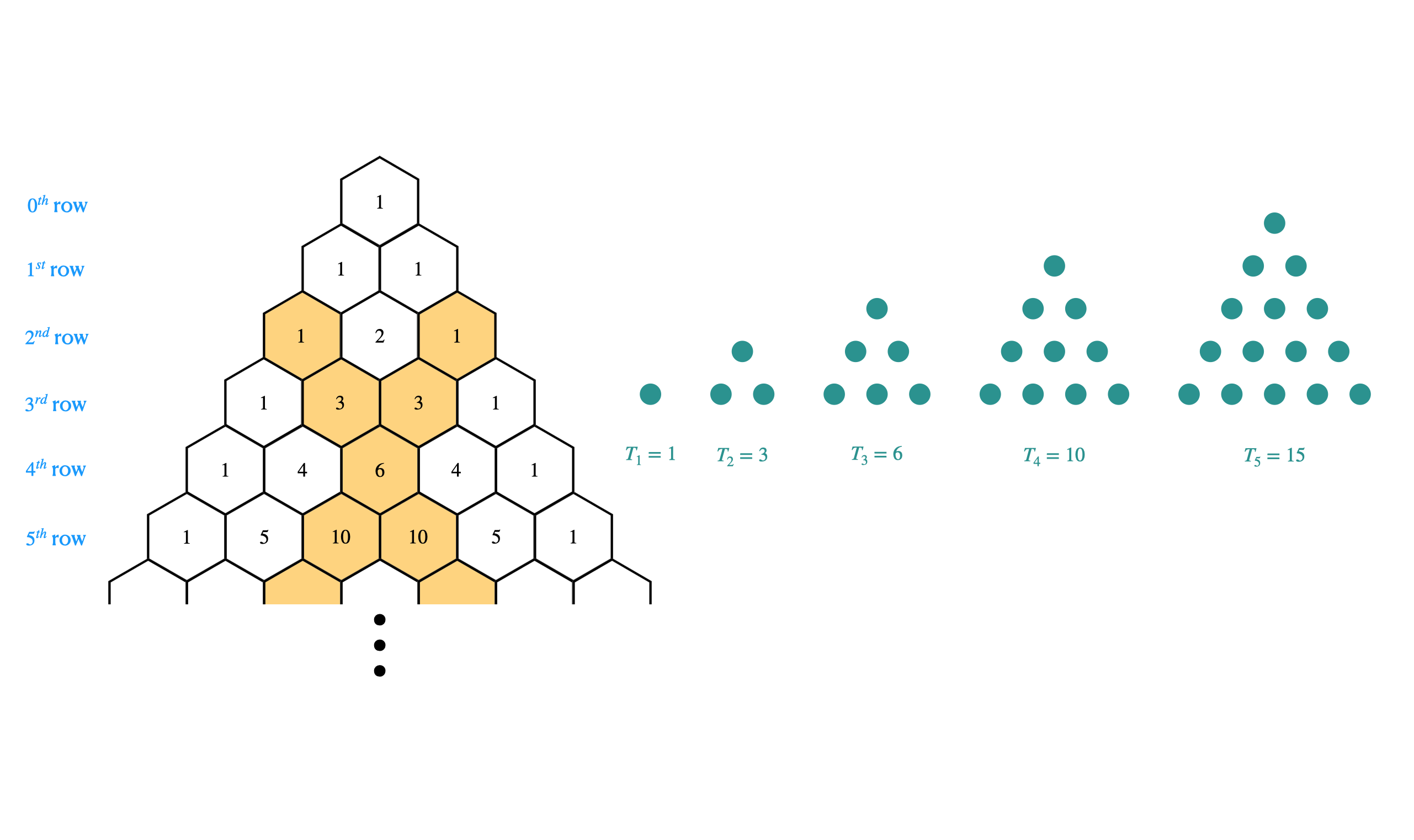
성질 4) 각 행을 모두 합한 수는 2의 거듭제곱과 같다.
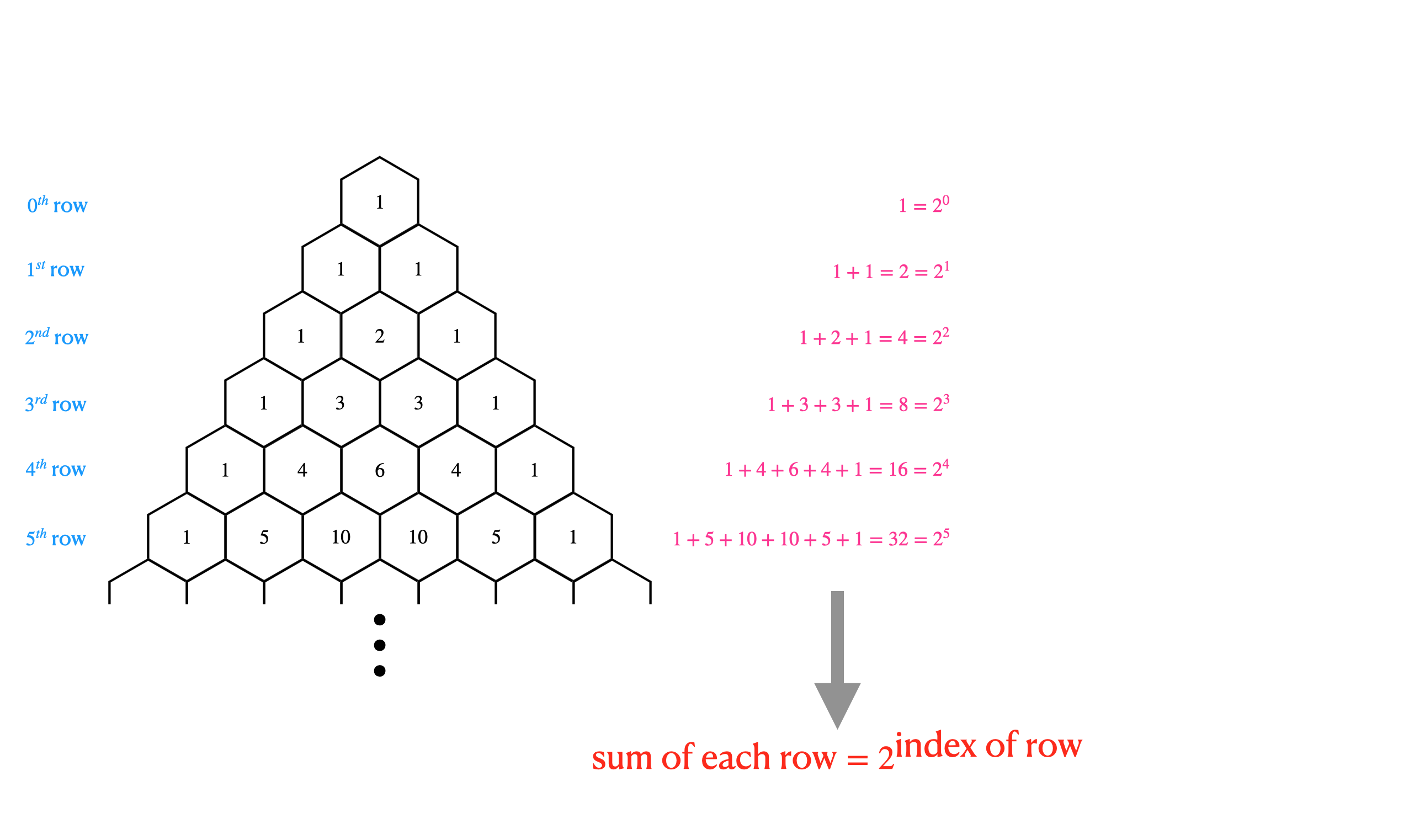
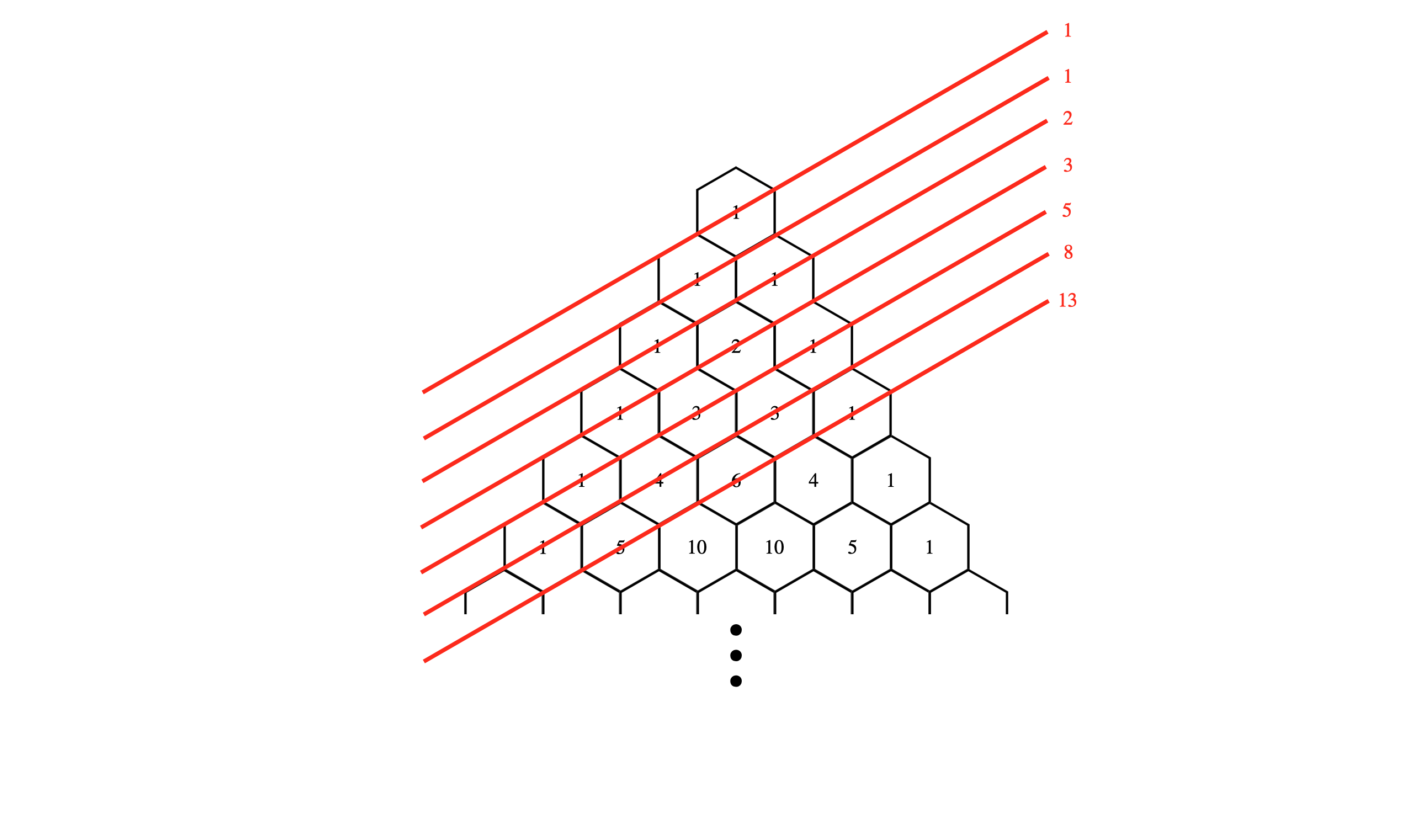
성질 5) 파스칼의 삼각형 안에는 피보나치 수열(Fibonacci sequence)이 숨어있다. (기울기가 30도인 직선을 사용하면 찾을 수 있다.)